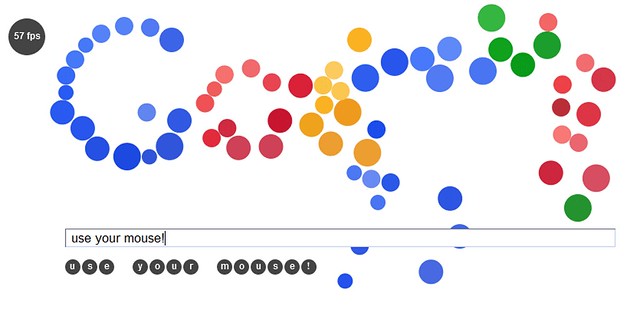
Interactive Google Doodle

Google’s take on an interactive ball logo was interesting enough to me that I felt that I needed to write something at least as fun. My take is backed by HTML5, so you will need a suitably compliant browser to view it.

Features

• Mass based ball collisions
• Mouse input to scatter balls
• Balls “anchored” to positions with dampened springs
• Typing creates additional interactable balls
• Searching cues exit animation

Technical information

The code for this demo (as well this entire blog) is on github. Here is the primary javascript engine.

In google’s original doodle, the balls would react with changes in size and velocity to the presence of the mouse. They would not, however, collide with anything. I thought this was a shame, and set out to make a HTML5 canvas app that could handle collisions between a large number of objects.

A naive initial implementation worked well enough. It looked like this (pseudocode is rubyish):

for i in 0 to circles.length - 2
for j in i + 1 to circles.length - 1
handleCollision(circles[i], circles[j]);
end
end

which served me well enough on Canary on my admittedly beefy desktop. It wasn’t until I tried to run the same on Firefox 3.x on my work laptop that I realized I probably wasn’t performant on a wide range of configurations.

The thing to do, then, was to set up a 2D grid covering the entire canvas. Each cell is about the diameter of a circle, and knows about any circles within itself, as well as up to four of its neighbors. Then, collision code becomes something like

for circle in circles
for potentialCollider in grid.getPotentialColliders(circle.pos)
handleCollision(circle, potentialCollider);
end
end

def grid.getPotentialColliders(pos)
cell = getCell(pos)
ret = []
for neighbor in cell.neighbors
ret = ret.concat(neighbor.objects)
end
ret
end

which takes the runtime complexity down from n^2 to about n. Neat!

Probably the hardest part was making circles appear for the query text. Understanding whether the user added characters, deleted, replaced, pasted, etc. is kind of difficult. I honestly hacked together a solution that works in 95% of use cases, but the best solution would to be to implement a full fledged dynamic programming algorithm to find the minimum edit distance.

And finally, a big thanks to Rob Hawke’s recreation of the google ball logo for both reference and initial source data points.