Above and Beyond the Affirm Job Puzzle

The latest startup from internet luminary Max Levchin recently launched, and they have a very entertaining programming puzzle up on their jobs page.

You should read the page for some background, but in summary the problem is to find the distances between any two cells in a hexagonal grid numbered in the following manner:

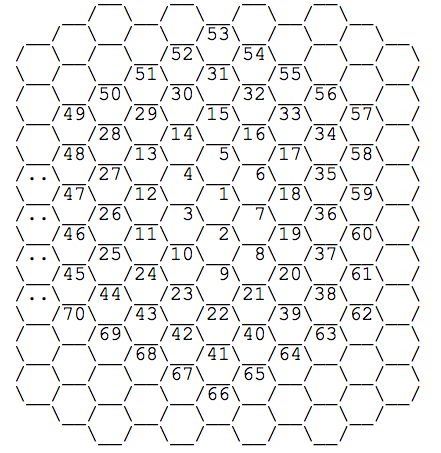
Approach

The problem is interesting because the problem seems like a traditional graph theory exercise, but Affirm hints that your solution should work at the scale of ten billion nodes. These two ideas don’t really jive, so one wonders if there’s an analytic solution that doesn’t involve any graph traversal.

It seems plausible that there is one, since the problem seems very similar to calculating the Manhattan Distance between any two nodes in a rectangular grid, except in this case we have a hexagonal grid where there are six ways to move between neighboring nodes instead of four. These six neighboring cells lie along three axes of movement.

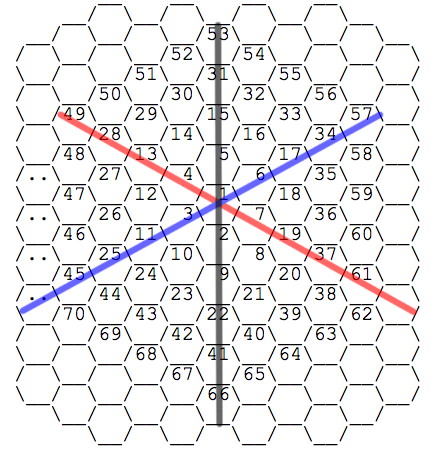
If you play around with the axes in your head, you can see that you can represent any hexagon in terms of any two of the three axes of movement. The corollary to that conclusion is that any translation down one axis of movement can be thought of as some combination of the other two. Essentially, we have one almost-unnecessary axis.

This suggests an approach:

• Turn a hex’s number into its grid coordinates
• Figure out the distance between two arbitrary grid coordinates

Translating a hexagon number into coordinates

Going from an arbitrary hexagon number to coordinates seems a bit tricky at first. You can’t modulo or divide by anything obvious to get some aspect of the geometry. The hex at position 1000 could be almost anywhere. What does seem obvious, though, is that higher numbers must be on larger “rings” of hexagons. Closer examination shows that each larger ring of hexagons has 6 more nodes than the last. Therefore:

$$ MaxNumOnRing(n) = ‎1 + ‎\sum\limits_{ring=0}^n 6ring \\ ... = 1 + 6\sum\limits_{ring=0}^n ring \\ ... = 1 + 6 \frac{n(n + 1)}{2} \\ ... = 3n^2 + 3n + 1 $$

The formula seems to check out, since the 0^th ring ends in 1, the 1^st ring in 7, the 2^nd ring in 19, and so on. Programmatically, you could tell which ring a hex falls on by finding which two “max-ring” numbers the hex is between. In the case of say, 12, it would be the 2^nd ring, since it is greater than 7 and less than 19. However, we can do better mathematically by simply inverting the previous formula, to get one that takes a number and outputs a ring:

$$ num = 3n^2 + 3n + 1 \\ num = 3(n^2 + n) + 1 \\ num = 3(n^2 + n + \tfrac{1}{4} - \tfrac{1}{4}) + 1 \\ num = 3((n + \tfrac{1}{2})^2 - \tfrac{1}{4}) + 1 \\ \frac{num - 1}{3} + \tfrac{1}{4} = (n + \tfrac{1}{2})^2 \\ \frac{4num - 1}{12} = (n + \tfrac{1}{2})^2\ \\ \sqrt\frac{4num - 1}{12} - \tfrac{1}{2} = n $$

Plugging in num = 10 gets us a ring number of ~1.3, which we round up to 2. Looks good! Now that we have the ring, we have to do the hard part: figure out where exactly on the ring we are. It also means we need to finalize our axes. I’ve illustrated the coordinate system I went with below. Why I choose this particular configuration should become clear later:

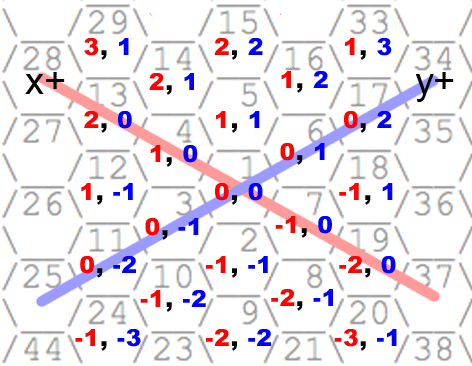
Following the pattern of coordinates here, you can see the largest number on each ring occurs on the negative X axis. Essentially we can say that if a number is the largest number on ring n, its position will be (0, -n). After a bit more thought, I figured that you could represent the various corners of the unit hexagon as six vectors that all pointed to hexagons exactly one away from the origin, like so:

require 'matrix'

UNIT_HEXAGON = {
  0 => Vector[-1,  0],
  1 => Vector[ 0,  1],
  2 => Vector[ 1,  1],
  3 => Vector[ 1,  0],
  4 => Vector[ 0, -1],
  5 => Vector[-1, -1]
}

You can get any number’s position along its hexagon ring by figuring out which of the six sides of the hexagon it is on, and its distance from the last corner of the hexagon.

def ring_to_max_num ring
  3 * ring**2 + 3 * ring + 1
end

def num_to_ring num
  (Math.sqrt((4 * num - 1) / 12.0) - 0.5).ceil
end

def num_to_coords num
  return Vector[0, 0] if num == 1

  # The length of a side is also the ring number
  side_length = ring = num_to_ring num

  # How far away am I from the end of my ring?
  offset = ring_to_max_num(ring) - num

  side_number = offset / side_length
  side_offset = offset % side_length

  corner = UNIT_HEXAGON[side_number]

  # The direction to the next corner is just the position of the
  # next corner minus the position of the current one.
  direction = UNIT_HEXAGON[(side_number + 1) % 6] - corner

  (corner * ring) + (direction * side_offset)
end

Solving for distance

So now we can easily get the grid coordinates of the start and end node. We still have to solve for the distance between them. A quick observation shows that the distance necessary to travel any delta vector is the same regardless of starting and ending nodes. That is to say, moving (+3, +2) units is the same distance whether you start at hex 1 or 1000. Luckily, with the axes I’ve chosen, calculating this distance isn’t too hard. At any given hexagon, you can move one unit along either the X or Y axes. You can also move one unit up or down the third axis, which is equivalent to moving by either (+1, +1) or (-1, -1). Our choice of axes has made that bit simple.

The process for finding the distance of a delta is:

• If the coordinates of the delta share a sign (both positive or negative), the distance is just the maximum of the absolute values of both coordinates. In moving (+3, +5), for instance, you move first to (+3, +3) in three moves, and then to (+3, +5) in another two for a total distance of five. The same is true of (-3, -5), with reversed directions.
• If they do not share a sign, merely add both of their absolute values together. For instance, moving (+2, -6) takes eight moves, because you have to move +2 in the X direction and -6 in the Y. Moving along the Z axis cannot aid you here.

def length_of_delta delta
  delta = -1 * delta if delta.all? {|i| i < 0}
  delta.all? {|i| i > 0} ? delta.max : delta.max - delta.min
end

def distance_between num1, num2
  delta = num_to_coords(num1) - num_to_coords(num2)
  length_of_delta delta
end

num1 = ARGV[0].to_i
num2 = ARGV[1].to_i
puts "distance between #{num1} and #{num2} is #{distance_between num1, num2}"

And viola, a constant-time algorithm that works fine at 10 billion nodes:

~/misc/affirm $ time ruby honeycomb.rb 1 100
distance between 1 and 100 is 6

real  0m0.030s
user  0m0.023s
sys 0m0.005s
~/misc/affirm $ time ruby honeycomb.rb 1 10000000000
distance between 1 and 10000000000 is 57735

real  0m0.030s
user  0m0.024s
sys 0m0.005s

Extra Credit

Solving for distance was nice, but honestly a bit anticlimactic. Wouldn’t it be more impressive if we could actually output the number of each hexagon on the way to our destination?

def path_between pos1, pos2
  delta = pos1 - pos2

  path = []

  while delta != Vector[0, 0]
    path.push(pos2 + delta)

    move = if delta.all? {|i| i < 0}
      Vector[1, 1]
    elsif delta.all? {|i| i > 0}
      Vector[-1, -1]
    elsif delta[0] != 0
      Vector[delta[0] > 0 ? -1 : 1, 0]
    else
      Vector[0, delta[1] > 0 ? -1 : 1]
    end

    delta += move
  end

  path.push pos2

  path
end

This function constructs a path of coordinates from pos1 to pos2, by attempting to move one hex at a time, favoring the Z axis where possible and otherwise just moving down the X or Y axes if there exists a remaining delta on either axis.

However, we still only have a path in coordinates. To get back to hexagon numbers, we need a translation function. This article is getting a bit long, so I’ll just leave it here as an exercise for the reader to puzzle out:

def coords_to_num pos
  return 1 if pos == Vector[0, 0]

  ring = [pos.max - pos.min : pos.map(&:abs).max].max

  side = if pos[0] == ring then 2
    elsif pos[0] == -ring then 5
    elsif pos[1] == ring then 1
    elsif pos[1] == -ring then 4
    elsif pos[0] > pos[1] then 3
    else 0
  end

  max_num = ring_to_max_num ring
  corner = UNIT_HEXAGON[side] * ring
  offset = side * ring + length_of_delta(pos - corner)
  offset == ring * 6 ? max_num : max_num - offset
end

Bring all the pieces together and you get…

~/misc/affirm $ ruby ../misc/affirm/honeycomb.rb 1 100
distance between 1 and 100 is 6
path is [1, 2, 9, 22, 42, 68, 100]

Magic! The runtime here is $O(\sqrt{n})$, because the path-finding algorithm is linear on the length of the path, and the path can only be as long as the square root of the largest hexagon number on the path. Recall that the ring of a hexagon number is a function of the square root of that number.

Thanks for the fun times, Levchin and co.